Question

What is the measurement of the largest angle in ΔABC such that a = 15 cm, b = 41 cm, and c = 29 cm? 135.0° 106.2° 50.0° 30.0°

Answer 1

From the given question

There are given that the sides of the triangle:

Now,

Find the first angle by using the cosine rule

So,

For angle A,

`a^2=b^2+c^2-2bc\cos A`

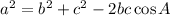
Then,

`\begin{gathered} a^2=b^2+c^2-2bc\cos A \\ 15^2=41^2+29^2-2*41*29*\cos A \\ 225^{}=1681+841-2378*\cos A \\ 225=2522-2378\cos A \\ -2297=-2378\cos A \\ \cos A=(2297)/(2378) \\ \cos A=0.96 \end{gathered}`

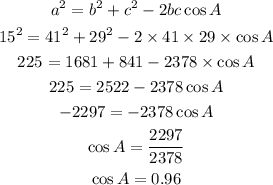
Then,

`\begin{gathered} A=\cos ^(-1)(0.96) \\ A=16.26 \end{gathered}`

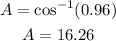
Now,

for the second angle B,

Use sine law:

So,

`\begin{gathered} (\sin A)/(a)=(\sin B)/(b) \\ (\sin16.26)/(15)=(\sin B)/(41) \\ \sin B*15=\sin 16.26*41 \\ \sin B=(\sin16.26*41)/(15) \\ \sin B=(11.5)/(15) \\ \sin B=0.76 \end{gathered}`

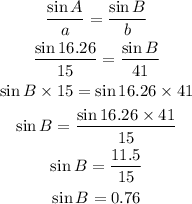
Then,

`\begin{gathered} \sin B=0.76 \\ B=135.0 \end{gathered}`

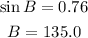
Now,

For the third angle:

`\begin{gathered} \angle A+\angle B+\angle C=180^(\circ) \\ 16.26+135+\angle C=180^(\circ) \\ \angle C=28.74 \end{gathered}`

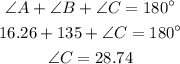
Hence, the correct option is A.