Question

A manufacturer produces both two-slice and four-slice toasters. The two-slice toaster takes 6 hours of labor to produce and the four-slice toaster takes 10 hours. The labor available is limited to 300 hours per week, and the total production capacity is 40 toasters per week.question: If the manufacturer decides to make 10 two-slice toasters, what is the maximum number of four-slice toasters they can make without going out of the time and production restrictions?

Answer 1

withoutLet "x" represent the two-slices toasters and "y" represent the four-slices toaster.

Each two-slice toaster takes 6hours to make and the four-slices takes 10 hours, you can express the total labor per week as:

`6x+10y=300`

The total capacity production is 40 toasters per week, so if you add the number of two-slice toaster and four-slice toasters made per week, they must add up to at most 40

`x+y\leq40`

To determine how many toasters they can make without exceeding the time restriction, replace the first expression with x=10 to determine the number of toasters you can make with out exceeding the time limit

`\begin{gathered} 6x+10y=300 \\ 6\cdot10+10y=300 \\ 60+10y=300 \\ 10y=300-60 \\ (10y)/(10)=(240)/(10) \\ y=24 \end{gathered}`

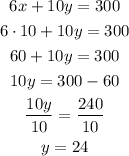
Without exceeding the time limit, the manufacturer can make 24 four-slice toasters.

Now you have to check if the value is within the production restrictions, remember that the manufacturer can produce up to 40 units per week, if the number of two-slice and four-slice toasters add up to 40 or less, then this restriction is not exceeded.

`x+y\leq40`

For x=10 and y=24

`\begin{gathered} 10+24\leq40 \\ 34\leq40 \end{gathered}`

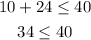
The production limit is not surpassed.

This means that if the manufacturer chooses to produce 10 two-slice toasters, he can produce 24 four-slice toasters without exceeding the time and production restrictions.