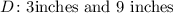Step-by-step explanation:
We are given the following details for a triangular prism;

Note that for the rectangular base, one side is 3 times the other. Hence, if the width is w, then the length would be 3 times w.
The surface area of a rectangular prism is;
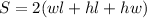
With the side lengths given we can now substitute and we'll have;
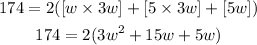
Divide both sides by 2;
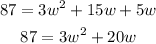
We shall now move all terms to one side of the equation;
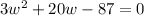
We can now solve this quadratic equationwith the quadratic equation formula;
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/rxvf73usjbbwyik14knxdemoz21vfz2ufc.png)
Where the variables are;
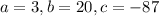
![w=\frac{-20\pm\sqrt[]{20^2-4(3)(-87)}}{2(3)}](https://img.qammunity.org/2023/formulas/mathematics/high-school/ktirorgvvwj12kco7lys0ldn6yb16nk1n9.png)
![w=\frac{-20\pm\sqrt[]{400+1044}}{6}](https://img.qammunity.org/2023/formulas/mathematics/high-school/rhp690g6dx7q6dqvpi9bu545bm8ewqyoi5.png)
![w=\frac{-20\pm\sqrt[]{1444}}{6}](https://img.qammunity.org/2023/formulas/mathematics/high-school/kpg3u4wj33jt1z52fsr9k5vcp3rydkg4z4.png)
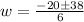
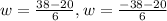
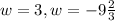
We now have two solutions. We shall take the positive one since our side lengths cannot be a negative value.
Therefore having the width as 3, the length which is 3 times the width is 3 times 3 and that gives 9.
Therefore;
ANSWER: