Question

What is the measure of z?zХГУ49Z =z = [?]VGive your answer in simplest form.Enter

Answer 1

In order to find the value of z, proceed as follow:

By using the Pythagorean theorem for the bigger triangle, you obtain:

`\begin{gathered} z^2=(4+9)^2-x^2 \\ z^2=13^2-x^2 \end{gathered}`

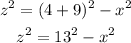
Now, if you consider the second bigger triangle:

`y^2=z^2-9^2`

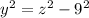
And in the smaller triangle:

`x^2=y^2+4^2`

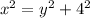
Next, replace the second equation for y^2 into the previous one:

`\begin{gathered} x^2=(z^2-9)+4^2^{} \\ x^2=z^2-9+4^2 \\ x^2=z^2-9+16=z^2+7 \end{gathered}`

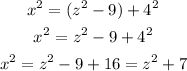
Now, replace the previous expression for x^2 into the first equation for z^2 and simplify:

`\begin{gathered} z^2=13^2-(z^2+7) \\ z^2+z^2=13^2+7 \\ 2z^2=169+7 \\ z^2=(176)/(2) \\ z^2=88 \\ z=\sqrt[]{88}=\sqrt[]{4\cdot22}=2\sqrt[]{22} \end{gathered}`

Hence, the value of z is 2√22