Question

What would the answer be and what step do i have to take to find true answer

Answer 1

Given:

There are given the equation:

`(1-3x)^{(1)/(2)}-1=x`

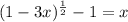
Step-by-step explanation:

According to the question:

We need to find the value of x.

So,

From the given equation:

`(1-3x)^{(1)/(2)}-1=x`

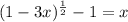
Then,

Add 1 to both sides of the equation:

So

`\begin{gathered} (1-3x)^{(1)/(2)}-1=x \\ (1-3x)^{(1)/(2)}=x+1 \end{gathered}`

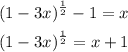
Then,

Square both sides of the above equation:

`\begin{gathered} (1-3x)^{(1)/(2)}=x+1 \\ (1-3x)=(x+1)^2 \\ (1-3x)=x^2+2x+1 \end{gathered}`

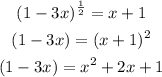
Then,

`\begin{gathered} 1-3x-x^2-2x-1=0 \\ -x^2-5x=0 \\ -x(x+5)=0 \\ x(x+5)=0 \end{gathered}`

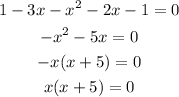
Then,

`\begin{gathered} x(x+5)=0 \\ x=0,x=-5 \end{gathered}`

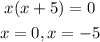
Final answer:

Hence, the correct option is C.