Given:
Diameter of the wheel = 26 inches
It rotates at 3 revolutions per second.
Let's find the linear speed of the wheel in feet/sec.
To find the linear speed, let's first find the circumference of the wheel.
Apply the formula:
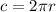
Where:
π = 3.14
r is the radius = diameter/2 = 26/2 = 13 inches
Hence, we have:
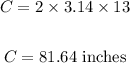
Now, to find the linear speed, we have:

Now, convert from inches/sec to feet/sec.
Where:
1 inch/sec = 0.0833333 ft/sec
Thus, we have:
244.9 in/sec = 244.9 x 0.0833333 = 20.4 feet/sec
Therefore, the linear speed in feet/sec is 20.4 feet/sec.
ANSWER:
20.4 feet/sec