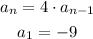Question

I need to find the expliciit and recursive formula for this problem I need help.

Answer 1

Notice that the sequence has a common ratio. To find it, divide the 2nd term over the 1st term:

`r=(-36)/(-9)=4`

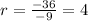
Verify that the same ratio is hold on the next terms:

`\begin{gathered} r=(-144)/(-36)=4 \\ r=(-576)/(-144)=4 \end{gathered}`

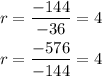
The explicit formula for the nth term of a sequence with first term a and common ratio r is:

`a_n=a\cdot r^(n-1)`

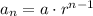
Then, the explicit formula for this sequence is:

`a_n=-9*4^(n-1)`

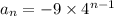
Since each term of the sequence is 4 times the previous term, then the recursive formula for this sequence, is:

`\begin{gathered} a_n=4\cdot a_(n-1) \\ a_1=-9 \end{gathered}`