Question

Find each trigonometric ratio. Give answer in the simplest form

Answer 1

Given the triangle below:

Required: To evaluate the trigonometric ratios for angles R and Q.

For angle R:

Step 1:

Name the sides of the above triangle with respect to the angle R.

`\begin{gathered} QR\Rightarrow hypotenuse\text{ (longest side of the triangle)} \\ QS\Rightarrow opposite\text{ (side opposite to the angle R)} \\ SR\Rightarrow adjacent \end{gathered}`

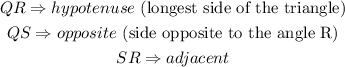
Step 2:

Evaluate the trigonometric ratios with respect to the angle R.

From the trigonometric ratios,

`\begin{gathered} \sin \text{ R = }(opposite)/(hypotenuse)\text{ = }(QS)/(QR) \\ \cos \text{ R = }(adjacent)/(hypotenuse)=(SR)/(QR) \\ \tan \text{ R = }(opposite)/(adjacent)=\text{ }(QS)/(SR) \end{gathered}`
`\begin{gathered} \text{where} \\ QR\text{ = 34, QS =16, SR = 30} \end{gathered}`

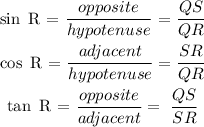
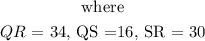
thus, evaluating for angle R, we have

`\begin{gathered} \sin \text{ R = }(opposite)/(hypotenuse)\text{ = }(QS)/(QR)\text{ = }(16)/(34) \\ \Rightarrow(8)/(17) \\ \cos \text{ R = }(adjacent)/(hypotenuse)=(SR)/(QR)=\text{ }(30)/(34) \\ \Rightarrow(15)/(17) \\ \tan \text{ R = }(opposite)/(adjacent)=\text{ }(QS)/(SR)=(16)/(30) \\ \Rightarrow(8)/(15) \end{gathered}`

For angle Q:

Step 1:

Name the sides of the above triangle with respect to the angle Q.

`\begin{gathered} QR\Rightarrow hypotenuse\text{ (longest side of the triangle)} \\ QS\Rightarrow adjacent \\ SR\Rightarrow opposite\text{ (side opposite the angle Q)} \end{gathered}`

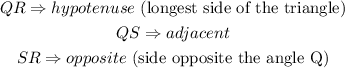
Step 2:

Evaluate the trigonometric ratios with respect to the angle Q.

From the trigonometric ratios,

`\begin{gathered} \sin \text{ Q = }(opposite)/(hypotenuse)\text{ = }(SR)/(QR) \\ \cos \text{ Q = }(adjacent)/(hypotenuse)=(QS)/(QR) \\ \tan \text{ Q = }(opposite)/(adjacent)=\text{ }(SR)/(QS) \\ \end{gathered}`
`\begin{gathered} \text{where} \\ QR\text{ = 34, QS =16, SR = 30} \end{gathered}`

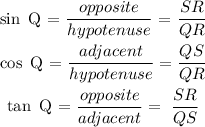
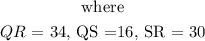
thus, evaluating for angle R, we have

`\begin{gathered} \sin \text{ Q = }(opposite)/(hypotenuse)\text{ = }(SR)/(QR)=(30)/(34) \\ \Rightarrow(15)/(17) \\ \cos \text{ Q = }(adjacent)/(hypotenuse)=(QS)/(QR)=(16)/(34) \\ \Rightarrow(8)/(17) \\ \tan \text{ Q = }(opposite)/(adjacent)=\text{ }(SR)/(QS)=(30)/(16) \\ \Rightarrow(15)/(8) \end{gathered}`

Hence,