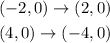Question

Please help me !! 1. f(x) = -(x+2)*(x-4)A new parabola , g(x) , is translated from f(x) using the translation T (-3,7) . What is the vertex point of g(x) ? Explain how you know . What are the x intercepts of the g(x) ? How did you figure it out ?

Answer 1

`\begin{gathered} Vg(x)=(-2,16) \\ \text{The x intercept are:} \\ (2,0)\text{ and }(-4,0) \end{gathered}`

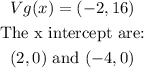
STEP-BY-STEP EXPLANATION:

The first thing we must do is calculate the vertex of f (x)

1.

`f(x)=-\mleft(x+2\mright)\cdot\mleft(x-4\mright)`

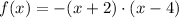
the vertex of an open top-down parabola of the form y = a * (x-m) * (x-n) is the average of its zeros, just like that:

`\begin{gathered} x=(m+n)/(2)=(-2+4)/(2)=1 \\ y=-1\cdot(1+2)\cdot(1-4)=9 \\ \text{The vertex is } \\ (1,9) \end{gathered}`

Now the vertex of g (x) would then be to apply the translation of (-3, 7) to the vertex of f (x)

`\begin{gathered} Vf(x)=(1,9)\rightarrow Vg(x)=(1-3,9+7)=(-2,16) \\ Vg(x)=(-2,16) \end{gathered}`

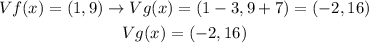
Then for the intercepts with x we must first calculate the intercepts in f (x)

`\begin{gathered} 0=-\mleft(x+2\mright)\cdot\mleft(x-4\mright) \\ 0=(x+2)\cdot(x-4) \\ x+2=0\rightarrow x=-2 \\ x-4=0\rightarrow x=4 \\ \text{Therefore, the x-intercept are:} \\ (-2,0)\text{ and}(4,0) \end{gathered}`

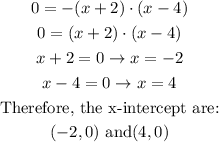
In the case of the x intercept in g (x), the signs of f (x) are exchanged, like this:

`\begin{gathered} (-2,0)\rightarrow(2,0) \\ (4,0)\rightarrow(-4,0) \end{gathered}`