Question

Last question choose from the correct choice A,BC, or D

Answer 1

Given the function

`R(x)=(7x+7)/(6x+12)`

we have to determine the behavior of the graph on either sides of the vertical asymptotes. if one exists.

Remember that vertical asymptotes occur when in a rational function, that is a function of the form

`R(x)=(f(x))/(g(x))`

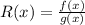
The denominator, g(x), becomes 0.

In our case, the denominator of the rational function is

`g(x)=6x+12`

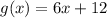
therefore

`6x+12=0\text{ }\Rightarrow\text{ }x=-2`

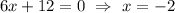
we conclude that there is a vertical asymptote at x=-2.

Now we will determine the behavior on both sides of the asymptote

One possible approach to discover this behavior is to pick up close to x=-2 values on both sides and evaluate it to determine the sign. Let us take

`x=-2.01\text{ and }x=-1.99`

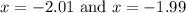
Evaluation the first one

`R(-2.01)=(7(-2.01)+7)/(6(-2.01)+12)=117.83`

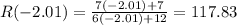
since the result is big and positive we conclude that on the left side of the asymptote the function approach to + infinity.

Now we will evaluate on the other side to determine the sign

`R(-1.99)=(7(-1.99)+7)/(6(-1.99)+12)=-115.5`

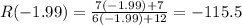
Therefore, the on the right the function approach to - infinity as the numbers approach to x=-2

Looking at the options we see that the correct option is the option c).