From the statement of the problem, we have:
• a right triangle △ABC,
,
• the altitude to the hypotenuse is denoted AN,
,
• AB = 2√5 in,
,
• NC = 1 in.
Using the data above, we draw the following diagram:
We must compute BN, AN and AC.
To solve this problem, we will use Pitagoras Theorem, which states that:

Where h is the hypotenuse, a and b the sides of a right triangle.
(I) From the picture, we see that we have two sub right triangles:
1) △ANC with sides:
• h = AC,
,
• a = ,NC = 1,,
,
• b = NA.
2) △ANB with sides:
• h = ,AB = 2√5,,
,
• a = BN,
,
• b = NA,
Replacing the data of the triangles in Pitagoras, Theorem, we get the following equations:
![\begin{cases}AC^2=1^2+NA^2, \\ (2\sqrt[]{5})^2=BN^2+NA^2\text{.}\end{cases}\Rightarrow\begin{cases}NA^2=AC^2-1, \\ NA^2=20-BN^2\text{.}\end{cases}](https://img.qammunity.org/2023/formulas/mathematics/college/8tyz15lvaizjm09hh721sqlmvwv3ecrt0s.png)
Equalling the last two equations, we have:
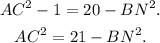
(II) To find the values of AC and BN we need another equation. We find that equation applying the Pigatoras Theorem to the sides of the bigger right triangle:
3) △ABC has sides:
• h = BC = ,BN + 1,,
,
• a = AC,
,
• b = ,AB = 2√5,,
Replacing these data in Pitagoras Theorem, we have:
![\begin{gathered} \mleft(BN+1\mright)^2=(2\sqrt[]{5})^2+AC^2 \\ (BN+1)^2=20+AC^2, \\ AC^2=(BN+1)^2-20. \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/844d4d9dc989vsleww1u5eyhlbagm1rxgw.png)
Equalling the last equation to the one from (I), we have:
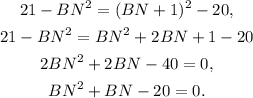
(III) Solving for BN the last quadratic equation, we get two values:
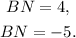
Because BN is a length, we must discard the negative value. So we have:

Replacing this value in the equation for AC, we get:
![\begin{gathered} AC^2=21-4^2, \\ AC^2=5, \\ AC=\sqrt[]{5}. \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/6dsdrg2i8fsvdytags8pbgucc16narrxvt.png)
Finally, replacing the value of AC in the equation of NA, we get:
![\begin{gathered} NA^2=(\sqrt[]{5})^2-1, \\ NA^2=5-1, \\ NA=\sqrt[]{4}, \\ AN=NA=2. \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/n08dmu4waythif9gwkujrzficxkupbt3ay.png)
Answers
The lengths of the sides are:
• BN = 4 in,
,
• AN = 2 in,
,
• AC = √5 in.