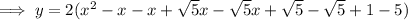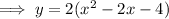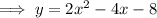Answer:
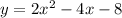
Explanation:
Factored form of a parabola
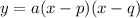
where:
- p and q are the x-intercepts.
- a is some constant.
Given x-intercepts:
Therefore:

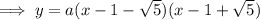
To find a, substitute the given point (4, 8) into the equation and solve for a:

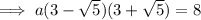
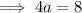
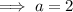
Therefore, the equation of the parabola in factored form is:
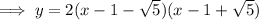
Expand so that the equation is in standard form: