Solution
Step 1:
The first two points are the roots of the parabola.
To get the roots of the parabola, equate y = 0
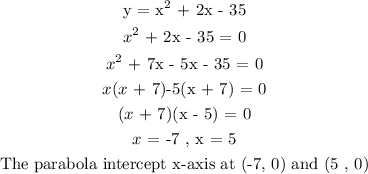
Step 2:
Find the y-intercept.
To find the y-intercept, plug x = 0
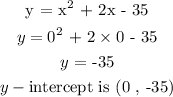
Step 3:
Find the vertex
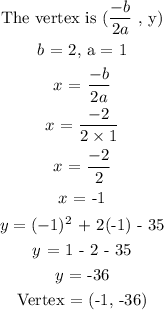
Final answer
All the five points are:
Roots (x-intercept) = (-7, 0) , (5 , 0)
y-intercept = (0, -35)
vertex = (-1, -36)
Other point = (-5, -20)