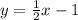Consider that the slope-intercept of a line is given by,
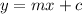
Here, 'm' is the slope and 'c' is the y-intercept of the line.
The equation of the given line is,
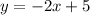
Comparing the coefficients, it can be observed that the slope of the given line is -2,
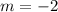
It is asked to determine the equation of line perpendicular line to this given line.
Let the slope of this perpendicular line be 'k'. Then, the equation of this perpendicular line will take the form,
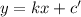
Theorem: The product of slopes of perpendicular lines is -1.
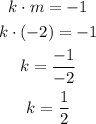
Now, the equation becomes,
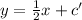
Consider that any point lying on the line must satisfy the equation of that line.
So the point (6,2) must also satisfy the equation of the perpendicular line,
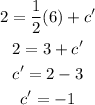
Substitute the values of 'k' and c' in the equation,
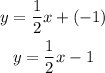
Thus, the required equation of the line is obtained as,