Question

Stephon has a square brick patio. He wants to reduce the width by 4 feet and increase the length by 4 feet.

Answer 1

We have that Stephon wants to reduce the width by 4, and we can represent this as follows:

`w=x-4`

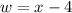
And he wants to increase the length by 4:

`l=x+4`

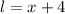
The square brick patio has an area of:

`A_{\text{squarepatio}}=20ft\cdot20ft=x\cdot x=400ft^2\Rightarrow x=20`

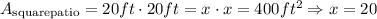
Therefore, the area of the new patio is given by:

`A=w\cdot l=(x-4)\cdot(x+4)`

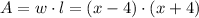
Since x = 20, we have:

`A=l\cdot w=(20-4)ft\cdot(20+4)ft\Rightarrow A=16ft\cdot24ft\Rightarrow A=384ft^2`

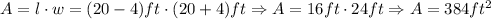
Therefore, the answer is A = 384 square feet (option C).