we know that
An equilateral truangle has three equal length sides
so
If triangle ABC is an equilateral triangle
then
AB=BC=AC
so
step 1
Find out the distance AB
The formula to calculate the distance between two points is equal to
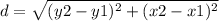
we have
A (-4,6)
B (6,6)
substitue in the formula

step 2
Find the distance BC
we have
B (6,6)
C( 1,-3)
substitute the values in the formula
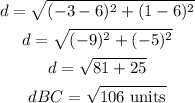
we have that
AB is not equal to BC
therefore
Is not an equilateral triangle
Is not necessary calculate the distance AC