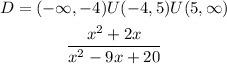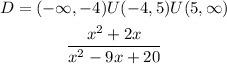
c) For this expression, let's start by rewriting it as a rational function:
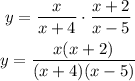
So to find out the Domain, we need to determine for which values do this function is defined. So looking at the denominator we can write out:
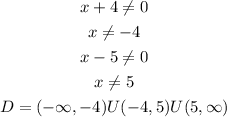
Note that if we plug into the denominator x=5 or x=-4 the function becomes undefined for the denominator would become equal to 0. For all values but -4, and 5 this function is defined.
We could draw the diagram to check the intersections.
2) Now, let's perform the product of that ratios, as indicated.
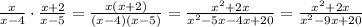
Note that when we multiply ratios we multiply both numerator and denominator simultaneously. We can leave it in its factored form as well.
3) Hence, the answer is: