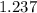Question

GPAs at CCSU are normally distributed with a mean of 2.27 and a standard deviation of 0.59. Find the z-score for a GPA of 3.

Answer 1

GIVEN:

We are given the following data and measures of central tendency;

`\begin{gathered} Mean(\mu)=2.27 \\ \\ Standard\text{ }deviation(\sigma)=0.59 \\ \\ GPA(x)=3 \end{gathered}`

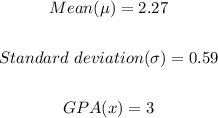
Required;

To find the z-score for a GPA of 3.0

Step-by-step solution;

The z-score will be determined by the formula;

`z-score=(x-\mu)/(\sigma)`

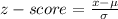
We now substitute the values and we have;

`\begin{gathered} z-score=(3-2.27)/(0.59) \\ \\ z-score=(0.73)/(0.59) \\ \\ z-score=1.23728813559 \\ \\ z-score\approx1.237 \end{gathered}`

ANSWER:

The fourth option is the correct answer.

`1.237`