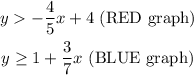To plot the line of the inequality , we begin by inserting the values x = 0 and y = 0 one after the other.

Letus now derive two points for the second inequality given just like we did for the first one above;
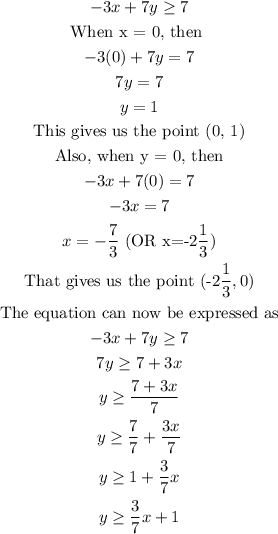
The graph of both inequalities is now shown below;
Observe carefully that the solution lies in the region shaded BLUE and RED.
One point in this region is (4, 4)
The blue and red graphs are represented by;