Question

Where are the minimum and maximum values for f(x) = sin x + 1 on the interval [0, 2π]?A. min:z =OB. min:x=OC. min:z =max:x= = 0, 2πOD. min:z = 0, π, 2π max: z =Reset Selectionmax: 1 =2 2max:z = 0, π, 2π

Answer 1

Given the function:

`f(x)=sinx+1`

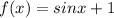
Let's find the minimum and maximum values over the interval [0, 2π].

Let's first find the derivative of the function:

`f^(\prime)(x)=cosx`

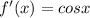
Now set the derivative to 0 and solve for x:

`\begin{gathered} cosx=0 \\ \\ \text{ Take the inverse cosine of both sides:} \\ x=cos^(-1)(0) \\ \\ x=(\pi)/(2) \end{gathered}`

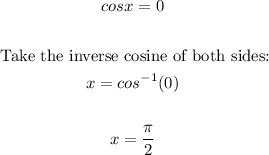
The cosine function is positive in quadrants I and IV, to find the reference angle(minimum), subtract the first solution from 2π:

`\begin{gathered} x=2\pi-(\pi)/(2) \\ \\ x=(2(2\pi)-\pi)/(2) \\ \\ x=(4\pi-\pi)/(2) \\ \\ x=(3\pi)/(2) \end{gathered}`

Plug in the values in the function to determine the minimum and maximum:

`\begin{gathered} f((\pi)/(2))=sin((\pi)/(2))+1=1+1=2 \\ \\ \\ f((3\pi)/(2))=sin((3\pi)/(2))+1=-1+1=0 \end{gathered}`

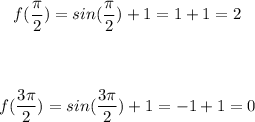
Therefore, we have the following:

Minimum occurs at: x = 3π/2

Maximum occurs at: x = π/2

ANSWER: