Remember that using radical notation, fractionary exponents can be represented as follows:
![a^{(n)/(m)}=\sqrt[m]{a^n}](https://img.qammunity.org/2023/formulas/mathematics/college/2zf6e1ptioq2zo561j3sln32lwzqvog40f.png)
On the other hand, when the index of a radical does not appear, we understand that it is equal to 2:
![\sqrt[]{a}=\sqrt[2]{a}](https://img.qammunity.org/2023/formulas/mathematics/high-school/o8j5ro2wt7sz57f4h2onfdqkhr3hqfma0k.png)
Rewrite each of the radical factors of the given expression using fractionary exponents:
![\sqrt[5]{x^3}\cdot\sqrt[]{x^4}=x^{(3)/(5)}\cdot x^{(4)/(2)}](https://img.qammunity.org/2023/formulas/mathematics/high-school/l42fclr5pedu7obcoa38l7xsjoil53rjei.png)
To simplify the expression, use the following rule of exponents:
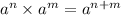
Then:
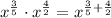
To simplify the expression, solve the addition with fractions:
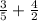
Simplify the fraction 4/2 as 2/1:
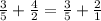
The leas common denominator for these fractions is 5. Rewrite 2/1 as 10/5 and add the fractions:
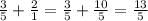
Then:
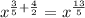
Therefore, the final expression in rational form, is:
![\sqrt[5]{x^3}\cdot\sqrt[]{x^4}=x^{(13)/(5)}](https://img.qammunity.org/2023/formulas/mathematics/high-school/wobtqwl6mgqjvzeawr25zl91rtaarmrmch.png)