Question

Hey! Been stuck on this problem, if anyone could helpThe officers of a high school senior class are planning to rent buses and vans for a class trip. Each bus can transport 70 students, requires 6 chaperones, and costs $1300 to rent. Each van can transport 10 students, requires 1 chaperone, and costs $80 to rent. Since there are 630 students in the senior class that may be eligible to go on the trip, the officers must plan to accommodate at least 630 students. Since only 60 parents have volunteered to serve as chaperones, the officers must plan to use at most 60 chaperones. How many vehicles of each type should the officers rent in order to minimize the transportation costs? What are the minimal transportation costs?The officers should rent how many buses and how many vans to minimize the transportation costs

Answer 1

hello

to solve this question, we need to write down details we have first in order to take some key facts into consideration.

1 bus (70 students + 6 chaperones) = $1300

1 van (10 students +1 chaperone) = $80

we have to take into consideration that the trip can only accomodate only 60 chaperone and also find the least expensive options to take.

the total number of students in senior class = 630 students

the best option would be to pick 7 buses and 15 vans

7 buses would be

`\begin{gathered} 7\text{ buses} \\ 70*7=490\text{ students} \end{gathered}`

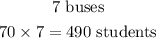
7 buses would accomodate 490 students and will require

`7(\text{buses)}*6\text{ chaperones }=42`

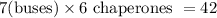
7 buses will accomodate 490 students and would require 42 chaperones.

now we would need at least 14 vans to accomodate the remaining students.

`\begin{gathered} 14\text{ buses} \\ 10(\text{students)}*14=140\text{ students} \end{gathered}`

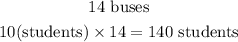
14 vans would require a total of 14 chaperones

`\begin{gathered} 7\text{ buses}=490\text{ students and 42 chaperones} \\ 14\text{ vans}=140\text{ students and 14 chaperones} \\ \text{total number of students = 630 students} \\ \text{total number of chaperones required = 42 + 14 =56} \end{gathered}`

now we can calculate the cost of the journey

`\begin{gathered} 1\text{ bus costs =\$1300} \\ 7\text{ buses = 7}*\text{ \$1300}=\text{ \$9,100} \\ 1\text{ van costs =\$80} \\ 14\text{ vans will cost = 14}*\text{ \$80}=\text{ \$1,120} \\ \text{total costs = \$9,100 + \$1,120}=\text{ \$10,220} \end{gathered}`

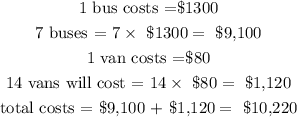
from the calculations above, the minimal cost of the journey is $10,220 and