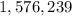Question

Use the pattern from part a to find the sum of the squares of the first 16 Fibonacci numbers

Answer 1

GIVEN:

We are given a Fibonacci sequence as shown in the attached image.

Required;

To use the pattern derived to find the sum of the squares of the first 16 Fibonacci numbers.

Step-by-step solution;

We have a Fibonacci sequence whose first term is 1.

The sequence and the sum of the squares of a given number of terms is derived as follows;

`\begin{gathered} 1^2+1^2=1*2 \\ \\ 1^2+1^2+2^2=2*3 \\ \\ 1^2+1^2+2^2+3^2=3*5 \\ \\ 1^2+1^2+2^2+3^2+5^2=5*8 \\ \\ 1^2+1^2+2^2+3^2+5^2+8^2=8*13 \\ \\ 1^2+1^2+2^2+3^2+5^2+8^2+13^2=13*21 \end{gathered}`

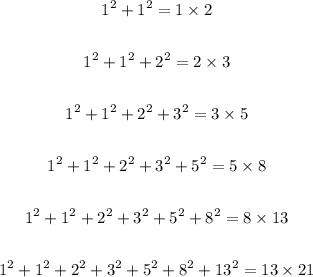
Next, we determine the sequence from the 1st to 16th term as follows;

`\begin{gathered} 1^2+1^2+2^2+3^2+5^2+8^2+13^2+21^2+34^2+55^2+89^2 \\ \\ +144^2+233^2+377^2+610^2+987^2=987*1597 \end{gathered}`

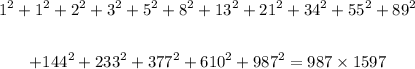
The sum of the squares of the first 16 terms therefore is

`987*1597=1,576,239`

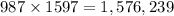
ANSWER:

`1,576,239`