To solve the equation below:
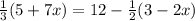
eliminate the denominators by multiplying each term on both sides of the equation by the least common denominator or the LCD. In this case, since the least common multiple of 3 and 2 is 6, the LCD must be 6.
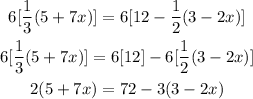
Eliminate the parentheses by distributing the numerical values outside the parentheses. In this case, we distribute the 2 to 5 and 7x and then distribute -3 to 3 and -2x.

Simplify both sides of the equation by combining like terms. Like terms are the terms with the same literal coefficients.
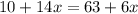
Isolate the variable terms by subtracting 6x and 10 from both sides of the equation.
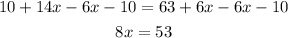
Solve for x by dividing both sides of the equation by 8.

Therefore, the value of x must be 53/8.