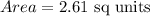Question

I have a calculus question about integration from my junior ap calculus class in high school. Pic included

Answer 1

Given: A function

`f(x)=√(x+2)`

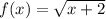
Required: To approximate the area between the x-axis and the curve between the interval [-1,1].

Step-by-step explanation: The area under the curve can be distributed into rectangles of width equal to the distance between the endpoints on the x-axis, and it is given that the height will be equal to the function's value at the left endpoint of each sub-interval.

We can divide the given interval into four sub-intervals as-

`[-1,1]=[-1,-0.5]\cup[-0.5,0]\cup[0,0.5]\cup[0.5,1]`

As we can see that the length of each interval is 0.5 units. Hence the width of each rectangle is 0.5 units.

Now we need to determine the height of each rectangle.

The height of rectangles can be determined by calculating the function's value at the left endpoint of each subinterval as follows-

`\begin{gathered} f(-1)=√(-1+2)=1 \\ f(-0.5)=√(-0.5+2)=√(1.5) \\ f(0)=√(0+2)=√(2) \\ f(0.5)=√(0.5+2)=√(2.5) \end{gathered}`

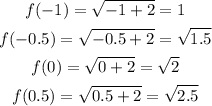
Hence the area is-

`Area=0.5f(-1)+0.5f(-0.5)+0.5f(0)+0.5f(0.5)`

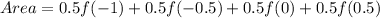
Substituting the values of the function and further solving as-

`\begin{gathered} Area=0.5(1+√(1.5)+√(2)+√(2.5)) \\ =2.61004\text{ sq units} \end{gathered}`

Final Answer: The area under the curve is-

`Area=2.61\text{ sq units}`