Question

Determine whether the two triangles are simllar. If they are similar, select the simllarity statement. А 24° 74° 0 B. C (select) of the angles in AABC are congruent to ZD, so the triangles (select) similar.

Answer 1

To solve the exercise you can first find the measure of angles B and C in triangle ABC.

Since the triangle ABC is an isosceles triangle, then it is true that

On the other hand, the Triangle Sum Theorem, which says that the sum of the three interior angles in a triangle is always 180°.

So, the measure of angles B and C in triangle ABC will be

`\begin{gathered} m\angle A+m\angle B+m\angle C=180\text{\degree} \\ 24\text{\degree}+m\angle B+m\angle B=180\text{\degree} \\ 24\text{\degree}+2\cdot m\angle B=180\text{\degree} \\ \text{ Subtract 24\degree from both sides of the equation}^{} \\ 24\text{\degree}+2\cdot m\angle B-24\text{\degree}=180\text{\degree}-24\text{\degree} \\ 2\cdot m\angle B=156\text{\degree} \\ \text{ Divide by 2 into both sides of the equation} \\ (2\cdot m\angle B)/(2)=\frac{156\text{\degree}}{2} \\ m\angle B=78\text{\degree} \\ \text{ Also} \\ m\angle C=78\text{\degree} \end{gathered}`

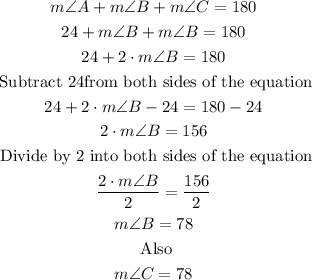
Then, you can see that none of the angles in triangle ABC is congruent with angle D.

`\begin{gathered} \angle B=78\text{\degree}\\e\text{ }74\text{\degree}\angle D \\ \angle C=78\text{\degree}\\e\text{ }74\text{\degree}\angle D \end{gathered}`

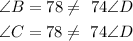
Therefore, none of the angles in triangle ABC are congruent to angle D, so the triangles are not similar.