Answer
The inverse of f(x) is:
![g(x)=\sqrt[]{x}-6\text{ (OPTION 1)}](https://img.qammunity.org/2023/formulas/mathematics/college/rxi2x8svhns3clbxepnz55ky602rib0idh.png)
Solution
The question asks us to find the inverse of the following function:
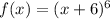
- For us to find the inverse of the function, we simply need to follow these steps:
1. Replace f(x) with y and make x the subject of the formula.
2. Substitute x for y and y for x in the expression gotten from step 1.
3. Replace y with g(x), which is the inverse of the function f(x)
- With the steps outlined above, we can proceed to solve the question:
Step 1
![\begin{gathered} f(x)=(x+6)^2 \\ \text{ Replace f(x) with y} \\ y=(x+6)^2 \\ \\ \text{Make x the subject of the formula} \\ \text{ Find the square root of both sides} \\ \sqrt[]{y}=x+6 \\ \\ \text{Subtract 6 from both sides} \\ x=\sqrt[]{y}-6 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/x4swimfrglawiry2xiwtsfy8ew6tyrhc2m.png)
Step 2:
![\begin{gathered} \text{The result from step 1 is:} \\ x=\sqrt[]{y}-6 \\ \\ \text{Exchange x for y and y for x} \\ y=\sqrt[]{x}-6 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/uoo2mqy0zk9wmgtkbdhpxpyyi4lldyvk1u.png)
Step 3:
![\begin{gathered} Th\text{e expression from step 2 is given by:} \\ y=\sqrt[]{x}-6\text{ } \\ \text{ Replace y with g(x)} \\ \\ \therefore g(x)=\sqrt[]{x}-6 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/38k3kd5ukgzw81yw7xk7jbsb09zlps6sx3.png)
Final Answer
The inverse of the function f(x) is given by:
![g(x)=\sqrt[]{x}-6\text{ (OPTION 1)}](https://img.qammunity.org/2023/formulas/mathematics/college/rxi2x8svhns3clbxepnz55ky602rib0idh.png)