Question

In LMN, point P is the centroid, and BP = 3. Find LP and BL

Answer 1

The value of LP and BL is 6 and 9 respectively. Option A is the right choice.

Since BP = 3, we can write BL = 3k for some positive constant k.

Then by the Centroid Theorem, AP = 2/3 BL=2k.

But we also know that AP =
`(AB + AM)/(2)`

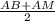
Since AB=AM, we have AP=AB=AM. Therefore, AB = AM = 2k.

Then by the Pythagorean Theorem,

`BL^2 = BP^2 + PL^2 = 3^2 + 2k^2 = 9 + 4k^2`

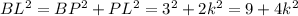
Substituting BL=3k, we get

`(3k)^2 = 9 + 4k^2`

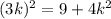
which simplifies to k= 3 / 4.

Hence, BL= 9 and LP = 6.

Final answer in 30 words:

BL=9, LP=6

​Option A is the right choice.

Answer 2

Second question

From the information given, P is the centroid of the triangle. The centroid theorem states that the centroid of the triangle is at 2/3 of the distance from the vertex to the midpoint of the sides. Considering the given triangle, it means that in triangle LMN,

LP = 2/3BL

LP + BP = BL

Given that BP = 3, then

LP + 3 = BL

2/3LB + 3 = LB

BL - 2/3BL = 3

1/3BL = 3

Multiply both sides by 3. We have

3 * 1/3LB = 3 * 3

BL = 9

LP = 2/3 * 9

LP = 6

Option A is correct