Two consecutive integers can be expressed as x, x+2, where x is the first odd integer.
Now, let's multiply these expressions and make them equal to 323, as the problem says.
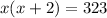
Let's solve for x

Once we have the quadratic equation, we use the quadratic formula
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/rxvf73usjbbwyik14knxdemoz21vfz2ufc.png)
Where a = 1, b = 2, and c = -323. Let's replace these values and solve
![\begin{gathered} x=\frac{-2\pm\sqrt[]{2^2-4\cdot1\cdot(-323)}}{2\cdot1} \\ x=\frac{-2\pm\sqrt[]{4+1292}}{2}=\frac{-2\pm\sqrt[]{1296}}{2} \\ x=(-2\pm36)/(2)=-1\pm18 \\ x_1=-1+18=17 \\ x_2=-1-18=-19 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/h15ie81f6pdmk3l1ncoqtgil4f4zgum7ft.png)
This means the two consecutive odd numbers are 17 and 19.
But also, -17 and -19 are solutions to the problem because they are integers whose product is 323.
Therefore, the solutions are {17,19} and {-17,-19}