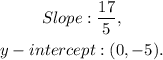Recall that the equation of a line in slope-intercept form is as follows:
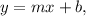
where m is the slope of the line and (0,b) is its y-intercept.
Adding 5y-25 to the given equation we get:
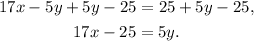
Dividing the above equation by 5 we get:
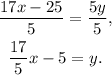
Then:
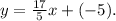
Therefore the slope of the given line is 17/5 and its y-intercept is (0,-5).
Answer: