Question

Step 1 of 2: Reduce the rational expression to its lowest terms 5xy + x^2/3x^2 + 4xStep 2 of 2: Find the restricted values of X, if any, for the given rational expression.

Answer 1

Step 1:

We have to reduce the expression:

`(5xy+x^2)/(3x^2+4x)`

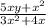
To do that we look at common factors between numerator and denominator, like the factor x:

`(5xy+x^2)/(3x^2+4x)=(x\cdot(5y+x))/(x\cdot(3x+4))=(5y+x)/(3x+4)`

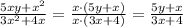
Step 2:

The restricted values of x are the ones that make the rational expression become undefined.

This can happen when the denominator, in this case 3x+4, becomes 0, so we can find the value of x as:

`\begin{gathered} 3x+4=0 \\ 3x=-4 \\ x=-(4)/(3) \end{gathered}`

The restricted value for x is -4/3.

Answer:

The reduced expression is (5y+x)/(3x+4).

The restricted value for x is x = -4/3.