The sum of the interior angles of a polygon is given by:
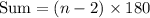
Where n is the number of sides of the polygon.
A regular 30-gon has 30 sides, then the sum is:
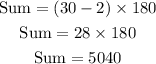
Now, we have to divide the total sum by the number of angles, then:
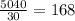
Answer: One interior angle of a regular 30-gon measures 168°.