Given:
The separation between the slits is,
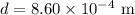
The distance between the slit and the screen is,
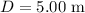
The separation between the central maximum and the first dark fringe is,
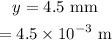
To find:
The wavelength of the light
Step-by-step explanation:
The diagram of the arrangement is shown below:
The separation between the central fringe and the mth bright fringe is,
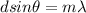
Here,
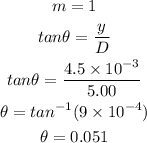
Now we can write,
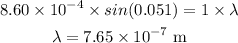
Hence, the wavelength is
