Question

A hunter aims directly at a target (on the same level as the arrow being shot) 38.0 m away. A) If the arrow leaves the bow at a speed of 23.1 m/s, by how much will it miss the target? B) At what angle should the bow be aimed in order to hit the target?

Answer 1

a) 13.25 m

b)22.3 degrees

Step-by-step explanation

Step 1

`\text{distance = velocity }\cdot time`

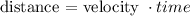
Let

`\begin{gathered} \text{distance = 38} \\ \text{time}=\text{ t} \\ \text{speed}=\text{ }23.1(m)/(s) \end{gathered}`

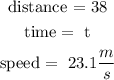
so

`\begin{gathered} \text{distance = velocity }\cdot time \\ 38\text{ m=23.1}\cdot t \\ t=\frac{38\text{ m}}{23.1}=1.645\text{ s} \\ \text{time}=\text{ 1.645} \end{gathered}`

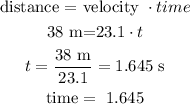
now , to find the disntace to the targe let's use the formula

`\begin{gathered} y=V_0\sin _{}\text{ (}\propto\text{)}+(1)/(2)gt^2 \\ as\text{ the angle is 0 } \\ y=V_0\sin _{}\text{ (0)}+(1)/(2)gt^2 \\ y=(1)/(2)gt^2 \end{gathered}`

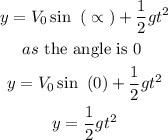
hence

`\begin{gathered} y_f=-(1)/(2)g\cdot t^2 \\ \text{replace} \\ y_f=-(1)/(2)(9.8)\cdot(1.645^2) \\ y_f=-(1)/(2)(9.8)\cdot(2.7) \\ y_f=-13.25 \\ \end{gathered}`

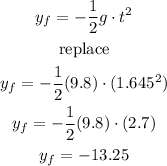
so,target missed by 13.25 meters.

Step 2

b)At what angle should the bow be aimed in order to hit the target?

to solve this we can use the expression

`\begin{gathered} t=\frac{dis\tan ce(x)}{velocity\text{ (x)}} \\ so \\ \text{distance}=\text{ 38 m} \\ V_x=V\text{ cos (}\propto) \\ V_x=23.1\text{ cos (}\propto) \\ \end{gathered}`

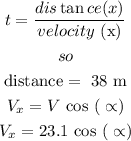
now, replace and solve for the angle

`\begin{gathered} t=\frac{dis\tan ce(x)}{velocity\text{ (x)}} \\ =(38)/(23.1\cos \propto) \\ \\ (38)/(23.1\cos\propto)=(23.1\sin \propto)/(4.9) \\ 38\cdot4.9=23.1\sin \propto\cdot23.1\cos \propto \\ (38\cdot4.9)/(23.1^2)=\sin c\propto\cos \propto \\ so \\ \propto=22.3 \end{gathered}`

so, the angle should be

22.3 degrees