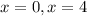Given the function below
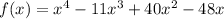
Where
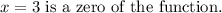
To find the other zeros,
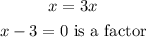
And x is common, factor out x, i.e

Divde the function by the factor x - 3
The quotient of the function after dividing by x - 3 is
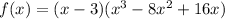
Factor out x
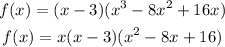
Factorize the remaining equation

To find the zeros of the above factored function, using the zero factor principle
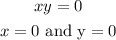
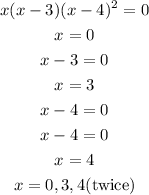
Hence, the othe two zeros of the function f(x) are