Question

The brand name of a certain chain of coffee shops has a 60% recognition rate in the town of Coffleton. An executive from the company wants to verify the recognition rate as the company is interested in opening a coffee shop in the town. He selects a random sample of 8 Coffleton residents. Find the probability that a. exactly 4 of the 8 Coffleton residents recognize the brand name. b. At least 4 residents recognized the brand. c. Find the mean and the standard deviation of the binomial distribution above.

Answer 1

Given:

`\begin{gathered} p=60\%=0.6 \\ n=8 \end{gathered}`

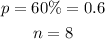
To Determine: The probability that (a) exactly 4 of the 8 Coffleton residents recognize the brand name.

Solution

Using binomial probability, the probability that exactly 4 of the 8 recognize the brand name is

`^8C_4p^4q^4`

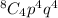
Note that

`\begin{gathered} P_r=^nC_rp^rq^(n-r) \\ q=1-p \\ q=1-0.6=0.4 \end{gathered}`

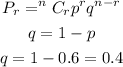
So,

`\begin{gathered} P_4=^8C_4*(0.6)^4(0.4)^4 \\ ^8C_4=(8!)/(4!4!)=(8*7*6*5*4!)/(4!*4*3*2*1)=(1680)/(24)=70 \end{gathered}`
`\begin{gathered} P_4=70*0.6^4*0.4^4 \\ P_4=0.2322432 \end{gathered}`

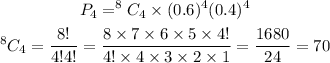
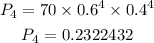
b) The probability of at least 4 residents recognized the brand

Using binomial distribution

`\begin{gathered} P(x\ge4)=P(4)+P(5)+P(6)+P(7)+P(8) \\ P(x\ge4)=0.2322432+0.27869+0.209018+0.08958+0.0168 \\ P(x\ge4)=0.82632 \\ P(x\ge4)\approx0.826 \end{gathered}`

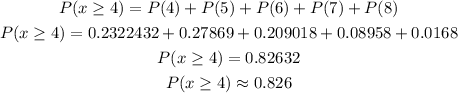
(c) Find the mean and the standard deviation of the binomial distribution

`\begin{gathered} Mean=np \\ Mean=8*0.6 \\ Mean=4.8 \end{gathered}`
`\begin{gathered} Standard-deviation=√(npq) \\ Standard-deviation=√(8*0.6*0.4) \\ Standard-deviation=1.3856 \\ Standard-deviation\approx1.386 \end{gathered}`

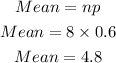
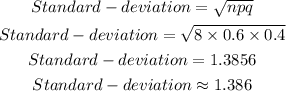
Hence, the probability that exactly 4 of the 8 Coffleton residents recognize the brand name is 0.232

(b) The probability that at least 4 residents recognized the brand is 0.826

(c) The mean is 4.8 and the standard deviation is 1.386