Question

What's the minimum and maximum of f(x)=-7x^2+700x

Answer 1

Given the function:

`f(x)=-7x^2+700x`

It is a parabola of the form:

`y=ax^2+bx+c`

Then the parameters of the given parabola are:

a = -7

b = 700

c = 0

We have that if a<0 then the vertex is a maximum value. In this case, a = -7, therefore the function has a maximum.

To find the maximum, we find the coordinate of the vertex, which is given by:

`x_(vertex)=-(b)/(2a)`

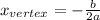
Substitute a and b:

`x_(vertex)=-(700)/(2(-7))=-(700)/(-14)=50`

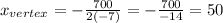
And we find y for the vertex:

`\begin{gathered} y_(vertex)=-7(50)^2+700(50)=-7(2500)+35000=-17500+35000 \\ =17500 \end{gathered}`

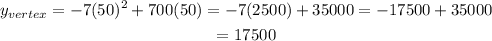
The vertex of the parabola is: (50, 17500) therefore the maximum is (50, 17500)

Answer:

maximum: (50, 17500)

minimum: none