Question

Determine the number of non-negative integers M that satisfy exactly three of the four statements below.(1) M is prime(2) M + 3 is prime(3) 1 < √ < 8(4) M + 5 has an odd number of factors

Answer 1

A non-negative integer is either positive or zero. It's the union of the natural numbers and the number zero.

A prime number is a number with only two factors, which are 1 and the number itself

Let consider the number

`2`

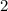
1) It satisfies the first statement

M is prime

2 is prime

2) M+3 is prime

since

`\begin{gathered} m=2 \\ 2+3=5\text{ } \\ 5\text{ is prime } \end{gathered}`

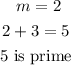
Hence

The second statement is satisfied

The third statement says

`\begin{gathered} 1<\sqrt[]{m}<8 \\ \text{which is } \\ 1<\sqrt[]{2}<8 \end{gathered}`
`\begin{gathered} \text{ since } \\ \sqrt[]{2}=1.414\ldots \\ \text{the third statement is satisfied } \end{gathered}`

Hence the third statement is satisfied

M=2

Since exactly 3 of the 4 statements is satisfied

From the second condition,

`M+3\text{ is prime }`

All prime numbers except 2 are odd numbers

Also,

The sum of two odds is even

`\text{let n be the prime numbers satisfying all the given conditions above }`

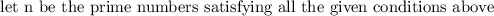
from the second condition,

M+3 is prime

`\begin{gathered} n+3\text{ is even } \\ \text{which contradicts the second conditions } \end{gathered}`

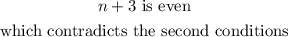
Hence

There is no other prime number that satisfies exactly three of the four conditions above

Therefore,

The number of non-negative integers that satisfy exactly three of the four conditions is 1

There is only one non-negative integer M which is 2 that satisfy the condition 1,2,3 above