Question

explain how properties of equality can be used to determine the pair without having to find the solution set for each.

Answer 1

If two expressions are equal to each other, and you add the same value to both sides of the equation, the equation will remain equal. Then, in the first case, we can add -7 to both sides and get

`\begin{gathered} 2(x+1)=13-7 \\ 2(x+1)=6 \end{gathered}`

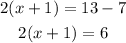
Similarly, in the second case, we can add -14 to both side and get

`\begin{gathered} 4(x+2)=26-14 \\ 4(x+2)=12 \end{gathered}`

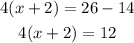
We can also divide both sides by the same quantity. In the first case, we can divide by 2 and ger

`\begin{gathered} x+1=(6)/(2) \\ x+1=3 \end{gathered}`

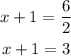
in the second case, we can divide by 4 and get

`\begin{gathered} x+2=(12)/(4) \\ x+2=3 \end{gathered}`

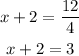
Finally, in the first case, we can add -1 to both side and get

`\begin{gathered} x=3-1 \\ x=2 \end{gathered}`

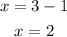
Similarly, in the second case, we can add -2 in both sides and get

`\begin{gathered} x=3-2 \\ x=1 \end{gathered}`

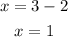
Then, in sumarry, you can add, substract, multiply or divide by the same number in both sides in order to remain the equallity of the given equation