Question

After opening an ancient bottle you find on the beach, a Djinni appears. In payment for his freedom, he gives you a choice of either 50,000 gold coins or one magical gold coin. The magic coin will turn into two gold coins on the first day. The two coins will turn into four coins total at the end of two days. By the end or the third day there will be eight gold coins total. The Djinni explains that the magic coins will continue this pattern of doubling each day for one moon cycle, 28 days. Which prize do you choose?When you have made your choice, answer these questions:The number of coins on the third day will be 2×2×2. Can you write another expression using exponents for the number of coins there will be on the third day?Write an expression for the number of coins there will be on the 28th day. Is this more or less than a million coins?

Answer 1

Geometric Sequences

I was given two choices:

* Take a 50,000 gold coins prize, or

* Take a 1 magic coin prize that doubles every day for 28 days.

Which prize do I choose? Clearly, the second choice. But that is because I already know the numbers behind geometric sequences.

Now I explain why by answering these questions:

1. The number of coins on the third day will be 2×2×2. It can be also expressed by using exponents as follows:

`2*2*2=2^3`

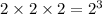
The exponent of the base 2 is the number of days that have passed.

For the 28th day, the magic coin will give:

`2^(28)\text{ coins}`

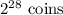
But we need to know how many coins have accumulated since the first day. This will be the result of the sum:

`S=1+2^1+2^2+2^3+2^4+\cdots+2^(28)`

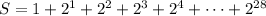
Given 1 equals 2 to the power of 0, we can write the sum as:

`S=2^0+2^1+2^2+2^3+2^4+\cdots+2^(28)`

This is the sum of a geometric sequence with a1 = 1 and a common ratio of r = 2.

The formula to compute the sum of n terms of a geometric sequence is:

`S_n=a_1\cdot(r^n-1)/(r-1)`

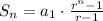
Since our sequence starts at n=0, there are n = 29 terms to sum:

`\begin{gathered} S_(29)=1\cdot(2^(29)-1)/(2-1) \\ S_(29)=536,870,911 \end{gathered}`

T