Question

#8A 90-foot rope from the top of a tree house to the ground forms a 45° angle of elevation from the ground. How high is the topof the tree house? Round your answer to the nearest tenth of a foot.feet

Answer 1

Given: A 90-foot rope from the top of a tree house to the ground forms a 45° angle of elevation from the ground.

Required: To determine the height of the tree house.

Explanation: The given problem can be represented as follows-

In the figure, AC represents the rope, and AB is the tree house. We need to determine the length of AB.

Recall the trigonometric ratio-

`sin\theta=(OppSide)/(Hypotenuse)`

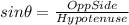
Thus, for triangle ABC we have-

`sinC=(AB)/(AC)`

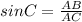
Substituting the values and solving for AB as-

`\begin{gathered} AB=90\cdot sin45\degree \\ =90*(1)/(√(2)) \\ =63.6396\text{ ft} \\ \end{gathered}`

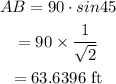
Thus,

`AB\approx63.6\text{ ft}`

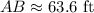
Final Answer: The top of the tree house is 63.6 ft high.