Answer: the volume of the body is1590.4m^3
This body is composed of a cillinder and two hemisferes. The two hemispheres forms an entire sphere, so we can calculate the volume of the cillinder and the volume of the sphere and add them up
Volume of the cillinder:

Volume of sphere:
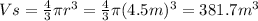
diameter=2*r so the radius is half the lenght of the diameter
now we add them up
