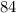The number of different combinations of k elements in a set of n elements, is:
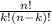
If we want to select three players from a group of 9 students, then the amount of different teams will be given by:
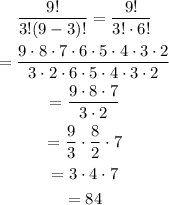
Therefore, the total amount of different teams that can be selected, is: