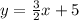Question

Write the equation of the line passing through the points (-4,-1) and (2,8). Show all of your work.

Answer 1

the general equation of the lines is

`y=mx+b`

where m is the slope and b the y-intercept

• calculating the slope

`\begin{gathered} m=(y2-y1)/(x2-x1) \\ \end{gathered}`

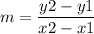
where (x2,y2) is a right point from (x1,y1)

on this case (x2,y2) is (2,8) and (x1,y1) the other point

replacing

`\begin{gathered} m=(8-(-1))/(2-(-4)) \\ \\ m=(9)/(6)=(3)/(2) \end{gathered}`

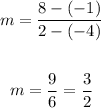
the slope is 3/2

• Calculating b

replace m and a point to solve b from the general equation. I will use the point (2,8)

`\begin{gathered} (8)=((3)/(2))(2)+b \\ 8=3+b \\ b=8-3 \\ b=5 \end{gathered}`

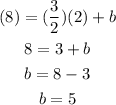
• rewriting the equation

replace m and b on the general equation

`y=(3)/(2)x+5`