Question

Suppose there is a 16.6% probability that a randomly selected person aged 25 years or older is a smoker. In addition, there is a 17.9% probability that a randomy selected person aged 25 years or older is male, given that he or she smokes. What is the probability that a randomly selected person aged 25 years or older is male and smokes? Would it be unusual to randomly select a person aged 25 years or older who is male and smokes?The probability that a randomly selected person aged 25 years or older is male and smokes is (Round to three decimal places as needed.).

Answer 1

We define the following events:

• A = a person aged 25 years or older is male,

,

• B = a person aged 25 years or older is a smoker,

• A | B = a person aged 25 years or older is male, ,given, that he or she smokes,

,

• A ∩ B = a person aged 25 years or older is male ,and, he or she smokes.

From the statement of the problem, we know that:

1) there is a 16.6% probability that a randomly selected person aged 25 years or older is a smoker, so we have:

`P\mleft(B\mright)=16.6\%=(16.6)/(100)=0.166,`

2) there is a 17.9% probability that a randomly selected person aged 25 years or older is male, given that he or she smokes, so we have:

`P(A|B)=17.9\%=(17.9)/(100)=0.179.`

Now, we know that the conditional probability P(A | B) is given by:

`P(A|B)=(P(A\cap B))/(P(B)).`

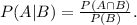
From the last equation, we have:

`P(A\cap B)=P(A|B)\cdot P(B).`

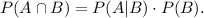
Replacing the values of P(A | B) and P(B), we get:

`P(A\cap B)=0.179\cdot0.166=0.029714\cong0.030.`

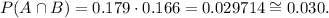
Answer

• So the probability that a randomly selected person aged 25 years or older is male ,and, smokes is ,0.030, in decimal form to three decimal places.

,

• So from 100 random persons, approximately 3 will be aged 25 years or older, male and smoker. We conclude that it will be unusual to randomly select a person with those atributes.