Answer:
the common difference is 2
and a₁ = 2
We need to find the first term given two terms of an arithmetic sequence:
a₆ = 12
a₁₄ = 28
First, we will solve for the common difference 'd'. To do this, we will create a system of equations using the given terms and the following formula:
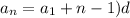
From the given, we can have:
![\begin{gathered} a_6=a_1+\operatorname{\lparen}6-1)d \\ 12=a_1+5d-------Eq1 \\ \end{gathered}]()
![\begin{gathered} a_(14)=a_1+\operatorname{\lparen}14-1)d \\ 28=a_1+13d \\ a_1=28-13d------Eq2 \end{gathered}]()
We will then substitute Eq.2 with Eq.1 to solve for the common difference 'd'
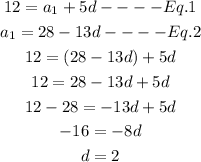
We now have a common difference d = 2
We can now solve the first term of the arithmetic sequence using any of the equations that we had. In this case, let us use Eq.2
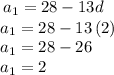
Therefore, the first term of the sequence is 2.