The triangle with side lengths 21, 28 and 35 can be solved in a number of ways. We shall attempt to solve it by using the Pythagoras theorem, and if the answer turns out correct, then its a right triangle.
The Pythagoras theorem states thus;
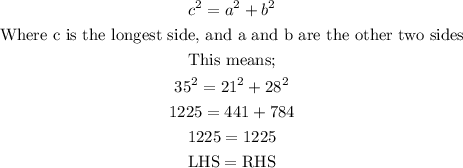
Since the Left hand side (LHS) equals the Right hand side (RHS), that means the given side lengths make a right angled triangle