Question

If sin(0)1213and O is in Quadrant III, then what is coss)

Answer 1

cos(θ/2) = -2(√2)/13

Step-by-step explanation:

To find cos(θ/2), we will use the following trigonometric identity

`\cos ((\theta)/(2))=\pm\sqrt[]{(1+\cos\theta)/(2)}`

Now, we know that sin(θ) = -12/13 and sin(θ) is also equal to the opposite side over the hypotenuse, so we can represent the angle with the following triangle

Then, using the Pythagorean theorem, we can find the value of the adjacent side x, so

`\begin{gathered} x=\sqrt[]{13^2-(-12)^2} \\ x=\sqrt[]{169-144} \\ x=\sqrt[]{25}=5 \end{gathered}`

Therefore, cos(θ) will be equal to:

`\cos (\theta)=\frac{\text{Adjacent}}{\text{Hypotenusa}}=(-5)/(13)`

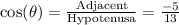
Where we use the negative sign because θ is in quadrant III. Now, we can use the trigonometric identity

`\begin{gathered} \cos ((\theta)/(2))=\pm\sqrt[]{(1+\cos\theta)/(2)}_{} \\ \cos ((\theta)/(2)_{})=\pm\sqrt[]{(1-(5)/(13))/(13)} \\ \cos ((\theta)/(2))=\pm\sqrt[]{(8)/(169)} \\ \cos ((\theta)/(2))=\pm\frac{2\sqrt[]{2}}{13} \end{gathered}`

Since θ is in quadrant III, θ/2 should be in quadrant II, so cos(θ/2) is negative. then, the answer is

`\cos ((\theta)/(2)_{})=-\frac{2\sqrt[]{2}}{13}`