When we are solving an equation the goal is to find the values which would make that equation equal to "0". Therefore if we have a quadratic equation of the following form:
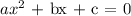
If it is possible to express it in a form with two perfect squares we can rewrite it as follows:
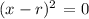
Where "r" is the root of the equation, its solution, therefore this would be the best method for solving it. Let's check an example:
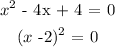
The answer to this quadratic equation is 2.