Question

During World War I, mortars were fired from trenches 3 feet below ground level. The mortars had a velocity of150 ft/sec. Determine how long it will take for the mortar shell to strike its target.• What is the initial height of the rocket? | Select ]• What is the maximum height of the rocket? | Select ]• How long does it take the rocket to reach the maximum height ? | Select]How long does it take the rocket to hit the ground (ground level)? [Select ]How long does it take the rocket to hit a one hundred feet tall building that is in it's downward path ?[ Select]What is the equation that represents the path of the rocket? | Select ]

Answer 1

The inital height of the rocket is -3 ft (since the mortar is 3 ft below ground)

To determine the maximum height of the rocket we have to remember the equation

`v^2_f-v^2_0=2a(s-s_0_{})`

where vf is the final velocity, v0 is the initial velocity, a is the acceleration (in this case the gravity), s is the final position and s0 is the initial position.

Since the maximum height is reach when vf=0, then we have

`0^2-(150)^2=2(-32.2)(y-(-3))`

Solving for y we have

`\begin{gathered} -((150)^2)/(2(-32))=y+3 \\ y=-((150)^2)/(2(-32))-3 \\ y=348.56 \end{gathered}`

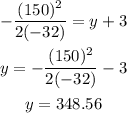
So the maximum height is 348.56 ft.

To determine the time it takes the rocket to reach the maximum height we have to remember the formula

`s=s_0+v_0t+(1)/(2)at^2_{}`

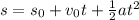
plugging the values we have:

`348.56=-3+(150)t+(1)/(2)(-32)t^2`

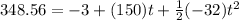
Solving the equation for t, we have

`\begin{gathered} 348.56+3=150t-16t^2 \\ 16t^2-150t+351.56=0 \\ \text{applying the general formula for quadratic equations we have } \\ t=\frac{-(-150)\pm\sqrt[]{(-150)^2-4(16)(351.56)}}{2(16)} \\ =\frac{150\pm\sqrt[]{22500-22500}}{32} \\ =\frac{150\pm\sqrt[]{0}}{32} \\ =(150\pm0)/(32) \\ \text{then} \\ t=4.6875 \end{gathered}`

therefore the time to reach the maximum height is 4.6875 s.

To find out how much time does the rocket take to hit the ground we have to use the same formula as before, only in this case s=0. Then

`\begin{gathered} 0=-3+150t-16t^2 \\ \text{solving for t we have} \\ t=\frac{-150\pm\sqrt[]{(150)^2-4(-16)(-3)}}{2(-16)} \\ =\frac{-150\pm\sqrt[]{22308}}{-32} \\ =(-150\pm149.3586)/(-32) \\ \text{then} \\ t_1=9.3549 \\ t_2=0.02 \end{gathered}`

therefore the time to reach the ground is 9.3549 s.